Introduction
En vision par ordinateur, l’objectif le plus courant est de classer une image (« chat », « chien », « voiture », etc.). Mais dans de nombreux cas, on cherche plutôt à comparer des images entre elles : retrouver des exemples similaires, regrouper des contenus, ou mesurer une proximité visuelle. Pour cela, nous voulons apprendre un espace de représentation (embedding) dans lequel les images similaires sont proches et les images différentes sont éloignées.
Dans la première partie de cette série d’article nous entrainerons un réseau siamois avec une triplet loss sur CIFAR‑10.
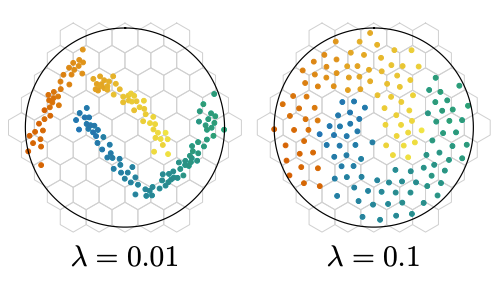
Nous étudierons ensuite la KoLeo loss, une régularisation dépendante du contenu du batch qui vise à mieux répartir les embeddings. Cette dépendance rend naturelle la question de l’accumulation de gradient (taille de batch effective) : quel impact sur l’entraînement et la qualité des embeddings ?
Nous commençons par décrire le dataset, la construction des triplets et l’évaluation, puis nous comparerons les résultats avec et sans KoLeo avant de discuter l’effet de l’accumulation du gradient.
Dans un premier temps, nous fixons les seeds pour la reproductibilité.
import numpy as np
import torch
seed = 42
def set_seed(seed):
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed)
if torch.mps.is_available():
torch.mps.manual_seed(seed)
set_seed(seed)
Le dataset utilisé
Pour entraîner et évaluer notre modèle, nous utilisons le jeu de données CIFAR‑10, un benchmark classique composé de 60 000 images couleur (32×32 pixels) réparties en 10 classes équilibrées : airplane, car, bird, cat, deer, dog, frog, horse, ship et truck. Le jeu est initialement séparé en 50 000 exemples d’entraînement et 10 000 exemples de test, mais ici nous n’utilisons que les données d’entraînement.
Après téléchargement, on remarque que l’archive contient 6 fichiers binaires : data_batch_1 à data_batch_5 et test_batch. Nous n’utiliserons que les fichiers data_batch_*.
import pickle
def unpickle(file):
with open(file, 'rb') as fo:
dict = pickle.load(fo, encoding='bytes')
return dict
data_batch = [unpickle(f"../cifar-10-python/data_batch_{i}") for i in range(1, 6)]
images = np.concatenate([data_batch[i][b'data'] for i in range(5)])
labels = np.concatenate([data_batch[i][b'labels'] for i in range(5)])
images = images.reshape((-1, 3, 32, 32)).transpose(0, 2, 3, 1)
images.shape
> (50000, 32, 32, 3)
Nous avons donc bien 50 000 images de taille 32×32 en RVB. En voici quelques-unes sélectionnées aléatoirement, avec leur classe.
import matplotlib.pyplot as plt
label_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
n_rows, n_cols = 3, 5
indices = np.random.choice(len(images), n_rows * n_cols, replace=False)
fig, axes = plt.subplots(n_rows, n_cols, figsize=(n_cols, n_rows))
for ax, idx in zip(axes.ravel(), indices):
ax.imshow(images[idx])
label = label_names[labels[idx]]
ax.set_title(label)
ax.axis("off")
plt.tight_layout()
plt.show()

Les réseaux siamois
Qu’est-ce qu’un réseau siamois ?
Un réseau siamois est une architecture de réseau de neurones conçue non pas pour prédire directement une classe, mais pour comparer des exemples entre eux.
L’idée clé est la suivante : deux images que l’on considère comme « similaires » (par exemple deux chiens) doivent être proches dans l’espace de représentation, alors que deux images « différentes » (un chien et une voiture) doivent être éloignées. Pendant l’entraînement, on présente donc au modèle des paires ou des triplets d’images (ancre, positive, négative) et l’on ajuste les poids pour rapprocher ancre et positive, tout en éloignant ancre et négative.

Dans la suite, nous détaillerons le modèle utilisé pour produire ces embeddings ainsi que la fonction de coût (la triplet loss) qui formalise cette notion de similarité.
VGG11
VGG11 est une architecture de réseau de neurones convolutifs proposée en 2014 par une équipe de l’université d’Oxford (Simonyan et Zisserman). L’idée majeure de la famille de réseau VGG est d’empiler de nombreux petits filtres convolutifs 3×3, séparés par des couches de pooling, plutôt que d’utiliser quelques grandes convolutions. Cela permet d’augmenter la profondeur du réseau tout en gardant une structure très régulière. Nous partirons de cette architecture pré‑entraînée sur ImageNet et nous l’adapterons pour produire des embeddings.

Voyons d’abord la taille du tenseur en sortie de VGG11.
from torchvision import models
vgg = models.vgg11(pretrained=False)
sample = images[0]
x = torch.from_numpy(sample).permute(2, 0, 1)
x = x.unsqueeze(0).float() / 255.0
with torch.no_grad():
out = vgg(x)
print("Taille du tenseur en sortie de VGG11 :", out.shape)
> Taille du tenseur en sortie de VGG11 : torch.Size([1, 1000])
La taille (1, 1000) signifie que, pour une image d’entrée, VGG11 renvoie un vecteur de 1 000 composantes. Ce nombre vient directement de la couche linéaire finale du modèle d’origine (FC-1000 puis Softmax sur le schéma) : VGG11 a été conçu pour attribuer une classe parmi 1000 à chaque image. Sa dernière couche produit donc un vecteur de 1 000 scores contenant les probabilités d’appartenance pour toutes les classes.
Dans notre cas, nous n’utiliserons pas ce vecteur. Nous utiliserons la sortie de la dernière couche de convolution, accessible via vgg.features.
Quelle est la taille du tenseur juste après la dernière couche de convolution ?
with torch.no_grad():
out = vgg.features(x)
print("Taille du tenseur en sortie de la dernière couche de convolution de VGG11 :", out.shape)
> Taille du tenseur en sortie de la dernière couche de convolution de VGG11 : torch.Size([1, 512, 1, 1])
On obtient un tenseur de forme (512, 1, 1).
512correspond au nombre de cartes de caractéristiques (features) produites par la dernière couche de convolution : 512 canaux décrivant l’image.(1, 1)correspond aux dimensions spatiales, réduites à 1×1 par la succession de convolutions et de pooling. Chaque canal résume donc l’image en une seule valeur avant de passer aux couches fully connected.
L’entrée de la couche linéaire a donc une dimension (512 x 1 x 1 = 512). Pour obtenir un vecteur d’embedding plus compact, nous projetons ensuite en dimension 128 via une couche linéaire. Enfin, nous ajoutons une couche de normalisation en sortie, utile pour les comparaisons entre embeddings.
import torch.nn as nn
import torch.nn.functional as F
class VGG11Embedding(nn.Module):
def __init__(self, pretrained):
super(VGG11Embedding, self).__init__()
vgg = models.vgg11(pretrained=pretrained)
self.features = vgg.features
self.linear = nn.Linear(512, 128)
def forward(self, x):
x = self.features(x)
x = torch.flatten(x, 1)
x = self.linear(x)
x = F.normalize(x, p=2, dim=1)
return x
Vérifions la taille en sortie de notre modèle :
vgg_embedding = VGG11Embedding(pretrained=False)
with torch.no_grad():
out = vgg_embedding(x)
print("Taille du tenseur en sortie de notre modèle :", out.shape)
> Taille du tenseur en sortie de notre modèle : torch.Size([1, 128])
Nous avons donc bien un embedding de taille 128.
La triplet loss
L’objectif de la triplet loss est d’imposer une structure géométrique à l’espace des embeddings : pour chaque triplet d’images (ancre, positive, négative), on veut que l’embedding de positive soit plus proche de celui de ancre que ne l’est celui de négative, avec une certaine marge. Autrement dit, on cherche à vérifier
$$ d(f(a), f(p)) + m < d(f(a), f(n)) $$
où \(f(\cdot)\) est le réseau d’embedding, \(d\) une mesure de distance et \(m > 0\) la marge.
Dans notre cas, nous utilisons une distance dérivée de la similarité cosinus : plus deux vecteurs sont proches angulairement, plus ils sont considérés comme similaires. La triplet loss s’écrit alors, pour un batch de taille \(B\), $$ \mathcal{L} = \frac{1}{B} \sum_{i=1}^B \max\big(0,\ d(a_i, p_i) - d(a_i, n_i) + m\big). $$
Chaque terme est nul dès que la contrainte est satisfaite (le triplet est « bon »). La valeur est strictement positive lorsque ancre est encore trop proche de négative. On ne veut donc pas seulement \(d(a_i, p_i) < d(a_i, n_i)\), mais une séparation d’au moins \(m\).
def triplet_loss(anchor, positive, negative, margin=0.4):
positive_distances = 1 - F.cosine_similarity(anchor, positive, dim=1)
negative_distances = 1 - F.cosine_similarity(anchor, negative, dim=1)
loss = torch.clamp(positive_distances - negative_distances + margin, min=0)
return loss.mean()
Construction des triplets
Pour entraîner un réseau siamois avec une triplet loss, nous devons transformer notre dataset d’images indépendantes en un dataset de triplets (ancre, positive, négative). Sur CIFAR‑10, nous procédons classe par classe :
- pour une classe donnée (par exemple « chat »), nous formons des paires (
ancre,positive) avec deux images de cette classe ; - nous tirons ensuite au hasard une image d’une classe différente pour jouer le rôle de
négative.
On répète cette opération pour chacune des 10 classes, ce qui donne un ensemble de triplets globalement équilibré. Le code ci‑dessous construit ces triplets à partir des tableaux images et labels et nous échantillonnons le nombre d’images négatives à 2 500.
triplets = np.empty((0, 3, 32, 32, 3), dtype=np.uint8)
triplets_labels = np.empty((0, 3), dtype=np.uint8)
set_seed(seed)
for target in range(10):
class_mask = (labels == target)
images_target = images[class_mask]
labels_target = labels[class_mask]
pairs = images_target.reshape(-1, 2, 32, 32, 3)
pos_labels = np.ones((len(pairs), 2), dtype=np.uint8) * target
not_target_mask = (labels != target)
images_not_target = images[not_target_mask]
labels_not_target = labels[not_target_mask]
# On echantillonne un nombre fixe de negatives pour cette classe
n_neg = min(2500, len(images_not_target))
neg_indices = np.random.choice(len(images_not_target), n_neg, replace=False)
negatives = images_not_target[neg_indices]
neg_labels = labels_not_target[neg_indices]
pairs = pairs[:n_neg]
pos_labels = pos_labels[:n_neg]
class_triplets = np.concatenate(
[pairs, negatives.reshape(n_neg, 1, 32, 32, 3)],
axis=1,
)
class_triplet_labels = np.concatenate(
[pos_labels, neg_labels.reshape(n_neg, 1)],
axis=1,
)
triplets = np.concatenate([triplets, class_triplets], axis=0)
triplets_labels = np.concatenate([triplets_labels, class_triplet_labels], axis=0)
triplets.shape, triplets_labels.shape
> ((25000, 3, 32, 32, 3), (25000, 3))
La classe TripletsCIFAR10Dataset et la visualisation des triplets
Pour faciliter l’entraînement, nous encapsulons ces triplets dans un Dataset dédié. Le tenseur de triplets est converti au format (N, 3, C, H, W) puis, à chaque appel, on renvoie les trois images (ancre, positive, négative).
from torch.utils.data import Dataset
import torchvision.transforms as T
class TripletsCIFAR10Dataset(Dataset):
def __init__(self, triplets, transform=None):
# (N, 3, H, W, C) -> (N, 3, C, H, W)
self.triplets = torch.from_numpy(
triplets.transpose(0, 1, 4, 2, 3) / 255.0
).float()
self.transform = transform
def __len__(self):
return self.triplets.shape[0]
def __getitem__(self, idx):
triplet = self.triplets[idx]
anchor, positive, negative = triplet[0], triplet[1], triplet[2]
if self.transform is not None:
anchor = self.transform(anchor)
positive = self.transform(positive)
negative = self.transform(negative)
return anchor, positive, negative
train_transforms = T.Compose([
T.RandomCrop(32, padding=4),
T.RandomHorizontalFlip(),
T.Normalize(mean=[0.4914, 0.4822, 0.4465], std=[0.2470, 0.2435, 0.2616]),
])
val_transforms = T.Compose([
T.Normalize(mean=[0.4914, 0.4822, 0.4465], std=[0.2470, 0.2435, 0.2616]),
])
Visualisons une sélection aléatoire de triplets.
n_examples = 5
indices = np.random.choice(len(triplet_dataset), n_examples, replace=False)
fig, axes = plt.subplots(n_examples, 3, figsize=(6, 1 * n_examples))
for row_idx, idx in enumerate(indices):
anchor, positive, negative = triplet_dataset[idx]
anchor_img = anchor.permute(1, 2, 0).numpy()
positive_img = positive.permute(1, 2, 0).numpy()
negative_img = negative.permute(1, 2, 0).numpy()
anchor_label = int(triplets_labels[idx, 0])
positive_label = int(triplets_labels[idx, 1])
negative_label = int(triplets_labels[idx, 2])
axes[row_idx, 0].imshow(anchor_img)
axes[row_idx, 0].set_title(f'anc: {label_names[anchor_label]}', fontsize=12)
axes[row_idx, 0].axis('off')
axes[row_idx, 0].set_ylabel(f'Triplet {idx}', fontsize=12, rotation=0, labelpad=50)
axes[row_idx, 1].imshow(positive_img)
axes[row_idx, 1].set_title(f'pos: {label_names[positive_label]}', fontsize=12)
axes[row_idx, 1].axis('off')
axes[row_idx, 2].imshow(negative_img)
axes[row_idx, 2].set_title(f'neg: {label_names[negative_label]}', fontsize=12)
axes[row_idx, 2].axis('off')
plt.tight_layout()
plt.show()

L’entraînement
Paramètres de l’entraînement
Pour entraîner notre réseau siamois avec la triplet loss, nous devons choisir quelques hyperparamètres clés :
- la taille de batch ;
- le taux d’apprentissage de l’optimiseur ;
- le nombre d’epochs ;
- la marge de la triplet loss.
Nous définissons également le device et choisissons Adam comme optimiseur.
if torch.cuda.is_available():
device = "cuda"
elif hasattr(torch.backends, "mps") and torch.backends.mps.is_available():
device = "mps"
else:
device = "cpu"
batch_size = 64
learning_rate = 5e-4
margin = 0.4
net = VGG11Embedding(pretrained=True).to(device)
optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)
Métriques d’évaluation
Nous utilisons les métriques suivantes pour évaluer le modèle sur la phase de validation :
- ratio de « bons » triplets : proportion de triplets où
ancreest plus proche depositiveque denégative; - similarités cosinus moyennes
ancre–positiveetancre–négative; - distances euclidiennes moyennes
ancre–positiveetancre–négative; - AUC.
AUC (Area Under the Curve)
L’AUC est l’aire sous la courbe ROC (Receiver Operating Characteristic), qui trace le taux de vrais positifs en fonction du taux de faux positifs pour tous les seuils possibles. Elle mesure la capacité du modèle à ordonner correctement les exemples : concrètement, c’est la probabilité qu’un exemple positif reçoive une similarité plus élevée qu’un exemple négatif. Une AUC de 0,5 correspond à un classement au hasard, tandis qu’une AUC de 1 indique une séparation parfaite.
Dans notre contexte, le réseau produit des embeddings (et non des probabilités de classe). Pour calculer l’AUC, on se ramène à une tâche binaire paire-à-paire : on considère (ancre, positive) comme paire positive (label 1) et (ancre, négative) comme paire négative (label 0). La similarité cosinus entre embeddings sert de score, et l’AUC résume à quel point le modèle attribue des similarités plus élevées aux paires de même classe.
Boucle d’entraînement
La boucle d’entraînement parcourt le DataLoader de triplets, calcule les embeddings (f(a), f(p), f(n)) pour chaque batch, évalue la triplet loss, puis effectue une étape de rétropropagation et de mise à jour des poids. Nous calculons également la loss moyenne par epoch et affichons périodiquement la loss courante pour suivre la convergence.
def train_loop(net, dataloader, optimizer, margin, print_freq=10):
net.train()
loss_accum = 0.0
epoch_loss = 0.0
for batch_idx, (anc, pos, neg) in enumerate(dataloader):
anc, pos, neg = anc.to(device), pos.to(device), neg.to(device)
anc_feat, pos_feat, neg_feat = net(anc), net(pos), net(neg)
loss = triplet_loss(anc_feat, pos_feat, neg_feat, margin)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_accum += loss.item()
epoch_loss += loss.item()
if (batch_idx + 1) % print_freq == 0:
print(f"Batch {batch_idx+1} : loss = {loss_accum / print_freq:.4f}")
loss_accum = 0.0
return epoch_loss / (batch_idx + 1)
Boucle de validation
Pour tout l’ensemble de validation, nous calculons les métriques définies plus haut (similarités cosinus, distances euclidiennes, ratio de bons triplets et AUC).
from sklearn.metrics import roc_auc_score
def validation_loop(net, dataloader, margin):
net.eval()
val_loss = 0.0
good_triplets = 0
total_triplets = 0
positive_similarities = []
negative_similarities = []
positive_euclidean_distances = []
negative_euclidean_distances = []
with torch.no_grad():
for batch_idx, (anc, pos, neg) in enumerate(dataloader):
anc, pos, neg = anc.to(device), pos.to(device), neg.to(device)
anc_feat, pos_feat, neg_feat = net(anc), net(pos), net(neg)
loss = triplet_loss(anc_feat, pos_feat, neg_feat, margin)
val_loss += loss.item()
batch_pos_euc = F.pairwise_distance(anc_feat, pos_feat, p=2)
batch_neg_euc = F.pairwise_distance(anc_feat, neg_feat, p=2)
positive_euclidean_distances.append(batch_pos_euc)
negative_euclidean_distances.append(batch_neg_euc)
batch_pos_sim = F.cosine_similarity(anc_feat, pos_feat, dim=1)
batch_neg_sim = F.cosine_similarity(anc_feat, neg_feat, dim=1)
positive_similarities.append(batch_pos_sim)
negative_similarities.append(batch_neg_sim)
good_triplets += (batch_pos_sim > batch_neg_sim).sum()
total_triplets += anc.shape[0]
positive_euclidean_distances = torch.cat(positive_euclidean_distances, dim=0)
negative_euclidean_distances = torch.cat(negative_euclidean_distances, dim=0)
positive_similarities = torch.cat(positive_similarities, dim=0)
negative_similarities = torch.cat(negative_similarities, dim=0)
scores = torch.cat([positive_similarities, negative_similarities], dim=0)
targets = torch.cat([
torch.ones_like(positive_similarities),
torch.zeros_like(negative_similarities)
], dim=0)
val_auc = roc_auc_score(targets.cpu().numpy(), scores.cpu().numpy())
return {
"val_loss": val_loss / (batch_idx + 1),
"val_auc": val_auc,
"mean_positive_similarities": positive_similarities.mean().item(),
"mean_negative_similarities": negative_similarities.mean().item(),
"mean_positive_euclidean_distances": positive_euclidean_distances.mean().item(),
"mean_negative_euclidean_distances": negative_euclidean_distances.mean().item(),
"good_triplets_ratio": (good_triplets / total_triplets).item(),
}
Entraînement complet sur plusieurs epochs
Pour entraîner un modèle, il nous faut construire nos DataLoader d’entraînement et de validation :
from torch.utils.data import DataLoader
val_split = 0.05
num_train = int((1 - val_split) * len(triplets))
shuffle_indices = np.random.permutation(len(triplets))
triplets = triplets[shuffle_indices]
triplets_labels = triplets_labels[shuffle_indices]
train_triplets = triplets[:num_train, ...]
val_triplets = triplets[num_train:]
train_labels = triplets_labels[:num_train, ...]
val_labels = triplets_labels[num_train:]
train_dataset = TripletsCIFAR10Dataset(train_triplets, transform=train_transforms)
val_dataset = TripletsCIFAR10Dataset(val_triplets, transform=val_transforms)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
Nous pouvons maintenant écrire la boucle d’entraînement complète : à chaque epoch, nous entraînons le modèle sur les triplets d’entraînement, puis nous calculons les métriques sur la validation.
Pour faciliter les expérimentations, nous sauvegardons régulièrement les poids. Nous sauvegardons également la configuration et les métriques de validation dans le dossier de l’expérience courante.
from datetime import datetime
import json
from pathlib import Path
runs_dir = Path('runs')
runs_dir.mkdir(exist_ok=True)
timestamp = datetime.now().strftime('%Y%m%d_%H%M%S')
save_dir = runs_dir / timestamp
save_dir.mkdir(exist_ok=True)
epochs = 15
save_ckpt_freq = 1
with (save_dir / "config.json").open("w") as fp:
json.dump({
"seed": seed,
"batch_size": batch_size,
"learning_rate": learning_rate,
"epochs": epochs,
"margin": margin,
"val_split": val_split,
"num_train": num_train,
"save_ckpt_freq": save_ckpt_freq
}, fp, indent=4)
import csv
metrics_path = save_dir / "training_metrics.csv"
train_losses = []
val_losses = []
best_auc = 0
best_epoch_path = None
csv_headers = [
"epoch",
"train_loss",
"val_loss",
"val_auc",
"mean_positive_similarities",
"mean_negative_similarities",
"mean_positive_euclidean_distances",
"mean_negative_euclidean_distances",
"good_triplets_ratio"
]
with open(metrics_path, mode='w', newline='') as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=csv_headers)
writer.writeheader()
set_seed(seed)
val_metrics = validation_loop(net, val_loader, margin)
print(f"Avant entraînement, epoch 0 — val_loss = {val_metrics['val_loss']}")
print(
f"Métriques de validation — "
f"val_loss: {val_metrics['val_loss']:.4f}, "
f"val_auc: {val_metrics['val_auc']:.4f}, "
f"mean_positive_similarities: {val_metrics['mean_positive_similarities']:.4f}, "
f"mean_negative_similarities: {val_metrics['mean_negative_similarities']:.4f}, "
f"mean_positive_euclidean_distances: {val_metrics['mean_positive_euclidean_distances']:.4f}, "
f"mean_negative_euclidean_distances: {val_metrics['mean_negative_euclidean_distances']:.4f}, "
f"good_triplets_ratio: {val_metrics['good_triplets_ratio']:.4f}"
)
with open(metrics_path, mode='a', newline='') as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=csv_headers)
writer.writerow({
"epoch": 0,
"train_loss": "", # No train_loss before training
"val_loss": val_metrics['val_loss'],
"val_auc": val_metrics['val_auc'],
"mean_positive_similarities": val_metrics['mean_positive_similarities'],
"mean_negative_similarities": val_metrics['mean_negative_similarities'],
"mean_positive_euclidean_distances": val_metrics['mean_positive_euclidean_distances'],
"mean_negative_euclidean_distances": val_metrics['mean_negative_euclidean_distances'],
"good_triplets_ratio": val_metrics['good_triplets_ratio']
})
for epoch_idx in range(epochs):
train_loss = train_loop(net, train_loader, optimizer, margin, print_freq=100)
val_metrics = validation_loop(net, val_loader, margin)
val_losses.append(val_metrics['val_loss'])
train_losses.append(train_loss if epoch_idx > 0 else val_metrics['val_loss'])
print(
f"epoch {epoch_idx+1} — "
f"train_loss = {train_loss:.4f}, "
f"val_loss = {val_metrics['val_loss']:.4f}"
)
print(
f"Métriques de validation — "
f"val_loss: {val_metrics['val_loss']:.4f}, "
f"val_auc: {val_metrics['val_auc']:.4f}, "
f"mean_positive_similarities: {val_metrics['mean_positive_similarities']:.4f}, "
f"mean_negative_similarities: {val_metrics['mean_negative_similarities']:.4f}, "
f"mean_positive_euclidean_distances: {val_metrics['mean_positive_euclidean_distances']:.4f}, "
f"mean_negative_euclidean_distances: {val_metrics['mean_negative_euclidean_distances']:.4f}, "
f"good_triplets_ratio: {val_metrics['good_triplets_ratio']:.4f}"
)
with open(metrics_path, mode='a', newline='') as csvfile:
writer = csv.DictWriter(csvfile, fieldnames=csv_headers)
writer.writerow({
"epoch": epoch_idx + 1,
"train_loss": train_loss,
"val_loss": val_metrics['val_loss'],
"val_auc": val_metrics['val_auc'],
"mean_positive_similarities": val_metrics['mean_positive_similarities'],
"mean_negative_similarities": val_metrics['mean_negative_similarities'],
"mean_positive_euclidean_distances": val_metrics['mean_positive_euclidean_distances'],
"mean_negative_euclidean_distances": val_metrics['mean_negative_euclidean_distances'],
"good_triplets_ratio": val_metrics['good_triplets_ratio']
})
if val_metrics['val_auc'] > best_auc:
best_auc = val_metrics['val_auc']
if best_epoch_path is not None:
best_epoch_path.unlink()
best_epoch_path = save_dir / f'best_epoch_{epoch_idx+1}.pth'
torch.save(net.state_dict(), best_epoch_path)
print(f"Nouvelle meilleure AUC : {best_auc:.4f} (epoch {epoch_idx+1})")
if (epoch_idx+1) % save_ckpt_freq == 0:
torch.save(net.state_dict(), save_dir / f'epoch_{epoch_idx+1}.pth')
Avant entraînement, epoch 0 — val_loss = 0.3092861518263817
Métriques de validation — val_loss: 0.3093, val_auc: 0.6764, mean_positive_similarities: 0.2754, mean_negative_similarities: 0.1793, mean_positive_euclidean_distances: 1.1962, mean_negative_euclidean_distances: 1.2766, good_triplets_ratio: 0.6928
Batch 100 : loss = 0.2213
Batch 200 : loss = 0.1943
Batch 300 : loss = 0.1630
epoch 1 — train_loss = 0.1872, val_loss = 0.1577
Métriques de validation — val_loss: 0.1577, val_auc: 0.8403, mean_positive_similarities: 0.7603, mean_negative_similarities: 0.2158, mean_positive_euclidean_distances: 0.5773, mean_negative_euclidean_distances: 1.1755, good_triplets_ratio: 0.8352
Nouvelle meilleure AUC : 0.8403 (epoch 1)
Batch 100 : loss = 0.1443
Batch 200 : loss = 0.1411
Batch 300 : loss = 0.1389
epoch 2 — train_loss = 0.1381, val_loss = 0.1381
Métriques de validation — val_loss: 0.1381, val_auc: 0.8643, mean_positive_similarities: 0.7282, mean_negative_similarities: 0.1812, mean_positive_euclidean_distances: 0.6405, mean_negative_euclidean_distances: 1.2281, good_triplets_ratio: 0.8616
Nouvelle meilleure AUC : 0.8643 (epoch 2)
Batch 100 : loss = 0.1181
Batch 200 : loss = 0.1119
Batch 300 : loss = 0.1102
...
epoch 15 — train_loss = 0.0337, val_loss = 0.0600
Métriques de validation — val_loss: 0.0600, val_auc: 0.9469, mean_positive_similarities: 0.7675, mean_negative_similarities: -0.0421, mean_positive_euclidean_distances: 0.5642, mean_negative_euclidean_distances: 1.4154, good_triplets_ratio: 0.9440
plt.figure(figsize=(8, 4))
plt.plot(train_losses, label="Loss (entraînement)")
plt.plot(val_losses, label="Loss (validation)")
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.legend()
plt.title("Évolution de la loss au cours de l’entraînement")
plt.show()

Visualisation de la courbe ROC et de l’AUC
Pour mieux interpréter les performances du modèle, nous traçons la courbe ROC (Receiver Operating Characteristic), qui représente le taux de vrais positifs en fonction du taux de faux positifs pour tous les seuils possibles. L’aire sous cette courbe (AUC) résume en un seul nombre la capacité du modèle à séparer les paires de même classe des paires de classes différentes.
Nous utilisons les données de validation pour construire cette courbe : les paires (ancre, positive) sont considérées comme positives (label 1) et les paires (ancre, négative) comme négatives (label 0). La similarité cosinus entre embeddings sert de score.
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
net.eval()
positive_similarities = []
negative_similarities = []
with torch.no_grad():
for batch_idx, (anc, pos, neg) in enumerate(val_loader):
anc, pos, neg = anc.to(device), pos.to(device), neg.to(device)
anc_feat, pos_feat, neg_feat = net(anc), net(pos), net(neg)
batch_pos_sim = F.cosine_similarity(anc_feat, pos_feat, dim=1)
batch_neg_sim = F.cosine_similarity(anc_feat, neg_feat, dim=1)
positive_similarities.append(batch_pos_sim)
negative_similarities.append(batch_neg_sim)
positive_similarities = torch.cat(positive_similarities, dim=0)
negative_similarities = torch.cat(negative_similarities, dim=0)
scores = torch.cat([positive_similarities, negative_similarities], dim=0).cpu().numpy()
targets = torch.cat([
torch.ones_like(positive_similarities),
torch.zeros_like(negative_similarities)
], dim=0).cpu().numpy()
fpr, tpr, thresholds = roc_curve(targets, scores)
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'Courbe ROC (AUC = {roc_auc:.3f})')
plt.fill_between(fpr, tpr, alpha=0.3, color='darkorange', label=f'Aire sous la courbe = {roc_auc:.3f}')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='Hasard (AUC = 0.5)')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Taux de faux positifs (FPR)')
plt.ylabel('Taux de vrais positifs (TPR)')
plt.title('Courbe ROC - Validation')
plt.legend(loc="lower right")
plt.grid(alpha=0.3)
plt.show()

Ici, nous ajoutons du code pour recharger le modèle si quelque chose se passe mal dans la suite du notebook.
# save_dir = Path("runs/20251213_224845")
# net.load_state_dict(torch.load(save_dir / 'best_epoch_2.pth'))
Conclusion
Dans cette première partie, nous avons présenté l’entraînement d’un réseau siamois sur CIFAR‑10 avec une triplet loss. Nous avons détaillé la construction du dataset de triplets, l’architecture du modèle basée sur VGG11, et la boucle d’entraînement complète avec ses métriques d’évaluation. L’entraînement montre une convergence satisfaisante avec une loss qui décroît régulièrement et des métriques de validation qui s’améliorent d’epoch en epoch.
Dans la suite de cette série, nous analyserons les embeddings obtenus en visualisant les résultats, puis nous introduirons la KoLeo loss pour encourager une répartition plus uniforme des embeddings, et nous étudierons l’impact de l’accumulation de gradient sur cette régularisation dépendante du batch.